私たちは、食べ物を消費することで生命維持をしたり、洗濯機や車を消費することで生活を便利にしたりなど、消費をすることで得られる何かのために消費をします。
そして経済学では、需要が存在するのは、消費者がその商品を消費することで幸福感を感じるからであるとされていて、消費者が財・サービスの消費によって得られる満足度を数値化したものを、「効用」と定義しています。
経済学では消費者の行動目標は、予算制約のもとで、効用の最大化することです。そして、財・サービスの消費量と効用の関係を表したものが、「効用関数」です。効用関数(曲線)は、英語で「効用」を意味するUtilityの頭文字から、Uと表記されることが一般的です。
参照(http://d.hatena.ne.jp/YoshifumiOkawa/20110115/1295051212)
そして効用関数の中でも同じ効用(=満足度)水準をもたらす消費点(= 2 財の消費量の組合せ)を結んだ曲線を無差別曲線といい、一般的に U(x,y)=xyという風に表記されます。
たとえば,同じ効用(=財の消費から得られる足度)が得られる 2 つの財(X財とY財)の消費量の組合せが下の表のようになっていたとすると、無差別曲線はしたのように表されます。


参照(https://online.lec-jp.com/images/goods/pdf/kd00413.pdf)
ここで、、片方の財の消費量が一定で、財の消費量が1単位増加したときに得られる効用の増加分のことを「限界効用」と言います。そして、無差別曲線は一般的に下のような形をしています。

無差別曲線の一般的な性質は
1.右下がり
2.原点に対し凸
3.右上の無差別曲線ほど効用が高い
4.効用水準の違う無差別曲線は絶対交わらない。
の4つです。
ちなみに、なぜ原点に凸のような形になるのかというと効用関数(無差別曲線)Uは基本的にU=xy と定義され、これを移項するとy=U/x となるので、y=1/xの反比例のグラフになるのと同様に、Uがどんな数値であっても基本的に効用関数(無差別曲線)Uは原点に凸の形になります。
そして、無差別曲線において大切な知識として限界代替率というのがあります。「限界代替率」とは、ある財の「消費量を1単位増加させたとき、同じ効用を保つために、もう一方の財を何単位減少させればよいか」を示したものです。
限界代替率をグラフで示すと、下のような無差別曲線に点に引いた接線の傾きになるので、効用関数を微分することで傾きを求めることが出来ます。
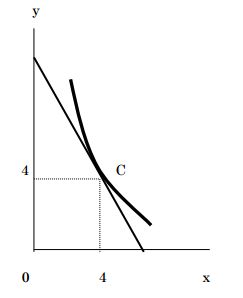
ざっくりまとめ
効用: 経済学において個人の満足度を表す概念
無差別曲線: 効用の等しい2財の量の組み合わせを意味する点を結んだ曲線
計算問題おいての効用関数=無差別曲線という認識でOKとまあ理屈はこんな感じですが、公務員試験とかでは計算できなければ意味がないので次は簡単な例題と解いていきます。
追記:ミクロ経済学を勉強する上で「絵でわかるミクロ経済学 (KS絵でわかるシリーズ)」が分かりやすかったのでオススメです。
関連記事




コメント