今回は経済学における「費用」の考え方について見ていきます。まず企業の製造する生産品に掛かる費用は「固定費用」と「可変費用」に分けられます。
まず固定費用とは生産品の数に関係なく一定に発生する費用の事で具体的には、機械の設備費や机などの備品に掛かる費用がこれにあたります。そして、可変費用とは生産量に依存する費用のことで、具体的には原材料費や人件費がこれにあたります。
総費用(TC:Total Cost)
固定費用+可変費用=総費用、生産にかかる費用全体のことで、生産量と総費用の関係は下のような曲線の関係で表されます。
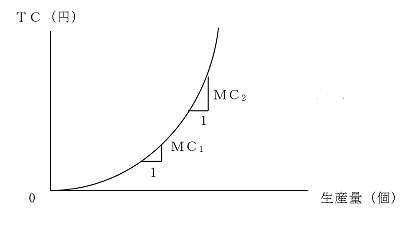
•限界費用(MC:Marginal Cost)
限界費用(MC)とは、総費用関数を生産量で微分したもので、生産品を1単位変化させたとき、それにかかる費用がどれだけ変化するのかというものを表したものです。限界費用をグラフで表すと下のような曲線になります。
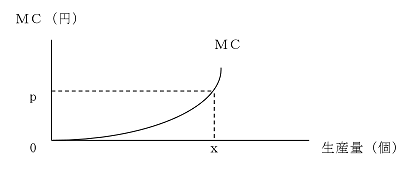
限界費用は生産量が増えるごとに上昇します。企業がある生産物を生産するときには価格と限界費用を比較してその是非を決定します。
そして理屈としては、価格が限界費用を上回る→生産を増やす→限界費用が上昇する(=限界費用が価格に近づく)→生産を増やし続け、価格と限界費用が一致すると、それ以上生産を増やさない。
限界費用が価格を上回る→生産を減らす→限界費用が低下する(=限界費用が価格に近づく)→生産を減らし続け、価格と限界費用が一致すると、それ以上生産を減らさない ということになります。
結果としては、この企業は、価格(p)=限界費用 (MC)となる生産量で、生産を行うとき利潤が最大化します。 (採算が合わないと、利益を最大化しても利潤がマイナスになることはがあります。)
平均費用(AC)
平均費用(AC)とは、総費用(TC)を生産量(x)で割ったもので、平均費用(AC)を、式を用いて表すと以下のようになります。
平均費用(AC)=総費用(TC)÷生産量(x)
例:総費用関数が下のように定義されているとき平均費用を求めよ。
TC(x)=x³-x²+2x+1
<解答>
平均費用は費用関数を生産量xで割ればよいから、
AC(x)=3x²-2x+2 となる。
企業の利潤最大化条件(計算問題に出てくるやつ)
上でも述べた通り、企業の利潤最大化条件は、価格(P)=限界費用(MC)。そして、価格=限界費用(P=MC)となるように生産量(x)を決定します。
ちなみに利潤を求めるときは総収入(TR)から総費用(TC)を差し引けばよいので、
利潤=総収入(TR)-総費用(TC)
となります。ここで、総収入(TR)は企業が価格受容者である限り、
総収入(TR)=価格(P)×生産量(x)
つまり、Pxとなります。
したがって、利潤を数式で表すと、利潤=Px-TCとなるので、これを最大化すればよい。つまり、利潤最大化するには、どのような場合であっても、微分して0になればよい。よって、利潤最大化は以下のような式が成立するとき達成されます。
・価格(P)-限界費用(MC)=0
・価格(P)=限界費用(MC)
また企業が独占・寡占といった不完全市場に存在している場合の利潤最大化条件は
限界収入(MR)=限界費用(MC)
となります。
次はここで独占企業における利潤最大化の簡単な例題を解いてみます。
追記:ミクロ経済学を勉強する上で「絵でわかるミクロ経済学 (KS絵でわかるシリーズ)」が分かりやすかったのでオススメです。
関連記事




コメント