標準正規分布について軽く説明したところで標準正規分布を使った確率の計算のやり方を解説していきます。
前回の復習ですが、標準正規分布とは、正規分布の確率変数を一定の式にし、確率密度関数を簡単な形にしたもののことをさします。
特徴としては平均が0、標準偏差1になります。そして、標準正規分布は下のような分布となります。
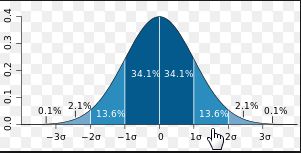
(参照:正規分布 – Wikipedia)
※μ=0、σ=1
標準正規分布で表せる数値は計算され、数値表になっており、t検定などで使用されています。また、正規分布から標準正規分布へ変換することを標準化といいます。
そして、標準正規分布表というのは下のような表です。
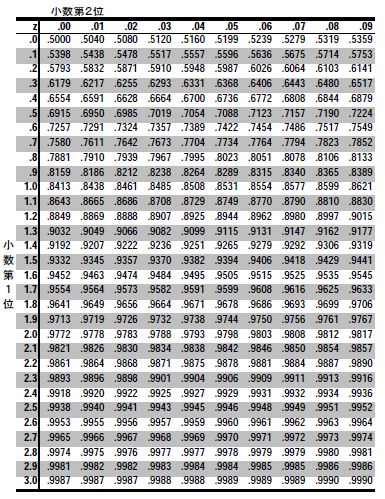
標準正規分布による確率計算
そして、確率変数Xを標準化したZに対応する確率Pの求め方は下のようになります。
・Xを標準化したZが0.62よりも小さくなる確率を求めるとき
P(Z < 0,62)
当てはまる数値は標準正規分布表のz = 0:6 の行と0:02 の列の交点なので、0,7324とわかり、Z< 0,62となる確率は約73%ということになります。
・確率変数Xを標準化したZが、-0.62≦Z≦0.62の範囲になる確率を求めるとき
P(-0:62 < Z < 0:62)
P(-0:62 < Z < 0:62) = P(Z < 0,62) - P(Z < -0,62) = 0,7324 -0,2676 = 0,4648
この変換は図で示すとわかりやすいです。

今度は逆にP(-a ≦ Z ≦ a) が0,5 となるaを求めたいとすると上図の斜線部分(全体の面積の50 %)の両端に位置するz 座標が知りたい。
両側なので、片側25 %ずつということで、P(Z ≦ z) = 0,75 のようなaを探すと早いです。左側でも問題なのですが、分布の右側で探すのが一般的です。
0,75 に1番近い数字を探す → 0,67 と0,68 の間ということになります。以下の範囲は推定や検定の信頼区間としてよく出てくるものです。
P(- 1,65 ≦ Z ≦ 1,65) → 0,90
P(- 1,96 ≦ Z ≦ 1,96) → 0,95
P(- 2,58 ≦ Z ≦ 2,58) → 0,99
まとめ
①:求めたデータを正規分布と仮定(近似)し、平均と分散・標準偏差を求める
↓
②:その正規分布を標準正規分布に変換し、確率変数XをZへと標準化する
↓
③:Z(変換した確率変数X)をとる確率を正規分布表を使って求める
という感じです。
追記:正規分布についてはコチラのPoint統計学 正規分布という本が分かりやすかったので紹介しておきます。
関連記事




コメント